MTE-40031: Biomedical Signal Processing and Analysing Assignment Help

Question
MTE-40031: This assignment for Keele University requires the student to write a structured report in order to demonstrate comprehension of the data processing and analysis listed in the assessment file. It is necessary for the student to use MATLAB for the data analysis, along with utilizing other requirements like a goniometer signal and two EMG signals. The complexity of this assignment makes it difficult for the Biomedical Engineering students to complete this assessment, which is why they trust OAS subject matter experts for this MSc Biomedical Engineering Assignment Help.
Solution
The solution to this assignment consists of a Biomedical Signal Processing Analysis done by our experts using MATLAB, as per the assessment file. In providing Keele University Assignment Help for this analysis, our experts have first loaded the raw data files and gave unique variable names to each of the columns. Then, the analysis was done, based on which all five questions were answered by our experts.
Question 1
The Repeated_Flexion_Extension and Fatigue_Trial files provided in the task file have been utilized to normalize the EMG data. Additionally, our experts have computed the envelopes of emg1_mvc and emg2_mvc first, and then determined each envelope’s maximum value.
% Calculate the envelopes of EMG1mvc and EMG2mvc
envelope_emg1_mvc = abs(hilbert(EMG1mvc));
envelope_emg2_mvc = abs(hilbert(EMG2mvc));
% Find the maximum values of the envelopes
max_envelope_emg1_mvc = max(envelope_emg1_mvc);
max_envelope_emg2_mvc = max(envelope_emg2_mvc);
Feeling stuck with this assignment? Don’t worry. Buy MTE-40031 assignment help from OAS at 25% off. WhatsApp us at +447700174710 today!
Question 2
The second question demands the student to eliminate any artifacts from the signals. This question is further divided into different sections:
Part A
In this part, our experts have utilized the Butterworth filter to describe the selection of cut-off frequencies and the rationale behind using a 4th order filter.
% Define the filter order and cutoff frequency
filter_order = 4; % Filter order
cutoff_freq = 100; % Cutoff frequency in Hz
sampling_freq = 1000; % Sampling frequency in Hz
% Compute the normalized cutoff frequency
normalized_cutoff_freq = cutoff_freq / (sampling_freq / 2);
Part B
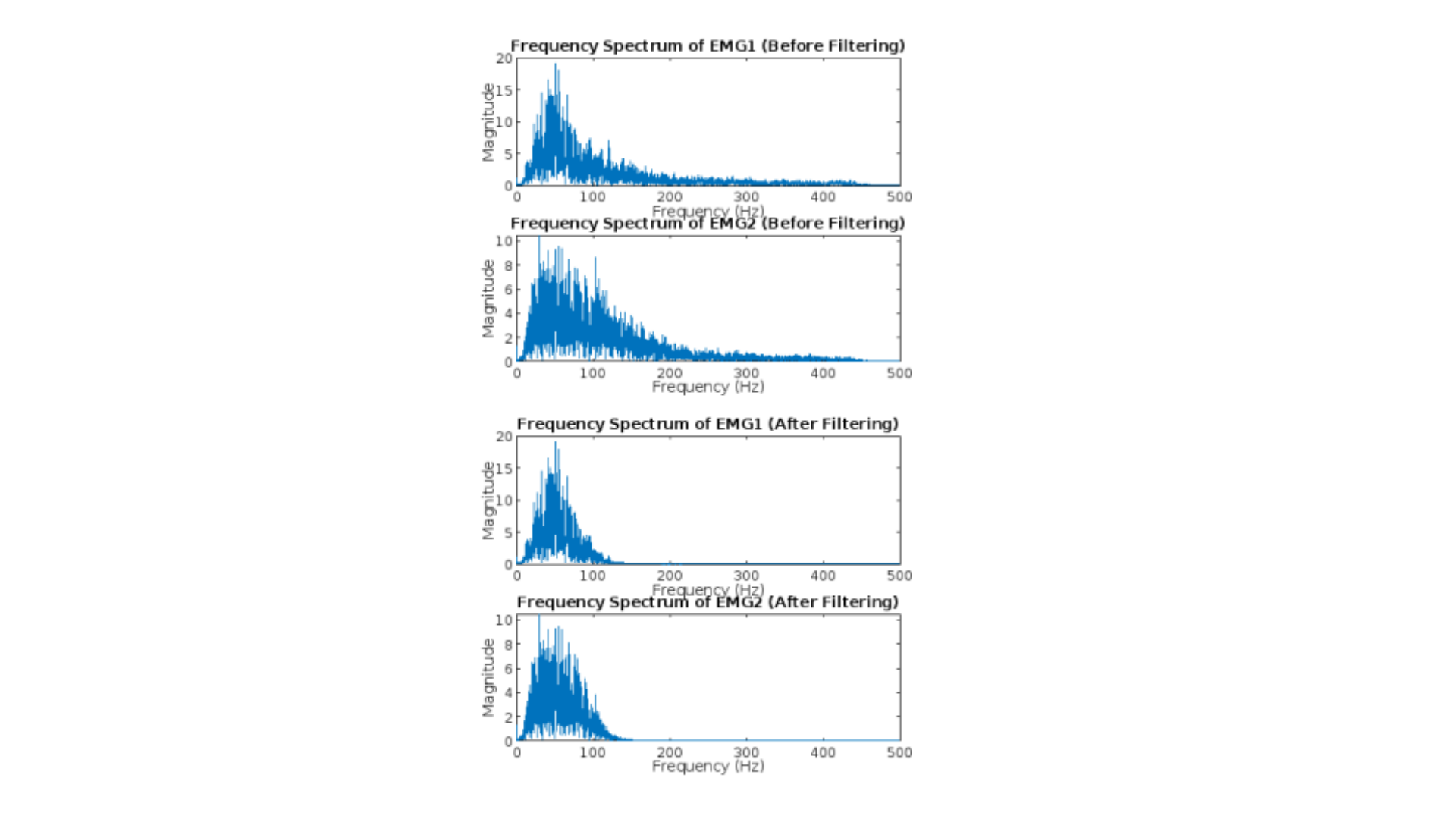
In providing MTE-40031 assignment help for this sub-section, our experts have examined and discussed the variations in frequency spectra prior to and following filtering.
% Compute the FFT of the normalized signals before filtering
fft_EMG1_before_filtering = fft(normalized_EMG1_Repeated_Flexion_Extension);
fft_EMG2_before_filtering = fft(normalized_EMG2_Repeated_Flexion_Extension);
% Compute the frequency axis for plotting
N = length(normalized_EMG1_Repeated_Flexion_Extension);
frequencies = (0:N/2-1) * (sampling_freq / N);
% Plot the frequency spectra before filtering
figure;
subplot(2,1,1);
plot(frequencies, abs(fft_EMG1_before_filtering(1:N/2)));
title(‘Frequency Spectrum of EMG1 (Before Filtering)’);
xlabel(‘Frequency (Hz)’);
ylabel(‘Magnitude’);
subplot(2,1,2);
plot(frequencies, abs(fft_EMG2_before_filtering(1:N/2)));
title(‘Frequency Spectrum of EMG2 (Before Filtering)’);
xlabel(‘Frequency (Hz)’);
ylabel(‘Magnitude’);
% Compute the FFT of the filtered signals
fft_EMG1_after_filtering = fft(filtered_EMG1_Repeated_Flexion_Extension);
fft_EMG2_after_filtering = fft(filtered_EMG2_Repeated_Flexion_Extension);
Part C
The last part of this question displays the raw and filtered signal versus time for each signal in the Repeated_Flexion_Extension and Fatigue_Trial data in a plot with two subplots. You can read a snippet of the complete solution below:
% Define the time axis
time_rfe = (0:length(EMG1rfe)-1) / sampling_freq;
time_ft = (0:length(EMG1ft)-1) / sampling_freq;
% Plot the raw and filtered signals from Repeated_Flexion_Extension
figure;
subplot(2,2,1);
plot(time_rfe, EMG1rfe);
title(‘Raw EMG1 – Repeated Flexion Extension’);
xlabel(‘Time (s)’);
ylabel(‘Amplitude’);
subplot(2,2,2);
plot(time_rfe, filtered_EMG1_Repeated_Flexion_Extension);
title(‘Filtered EMG1 – Repeated Flexion Extension’);
xlabel(‘Time (s)’);
ylabel(‘Amplitude’);
subplot(2,2,3);
plot(time_rfe, EMG2rfe);
title(‘Raw EMG2 – Repeated Flexion Extension’);
xlabel(‘Time (s)’);
ylabel(‘Amplitude’);
subplot(2,2,4);
plot(time_rfe, filtered_EMG2_Repeated_Flexion_Extension);
title(‘Filtered EMG2 – Repeated Flexion Extension’);
xlabel(‘Time (s)’);
ylabel(‘Amplitude’);
If you are looking for Biomedical Engineering assignment help, don’t hesitate to call us at +61 871501720.

Question 3
By comparing the timing of the EMG activity with the goniometer data from the Repeated_Flexion_Extension data, our highly skilled subject matter experts have determined which EMG signal was captured from each muscle. We provide a step-by-step analysis and a clear description of the results. This is how we provide the best biomedical engineering assignment help in England.
% Rectify the filtered EMG1 and EMG2 signals
rectified_EMG1 = abs(filtered_EMG1_Repeated_Flexion_Extension);
rectified_EMG2 = abs(filtered_EMG2_Repeated_Flexion_Extension);
% Obtain the upper envelope of each signal using the envelope function
[upper_env_EMG1, ~] = envelope(rectified_EMG1, 80, ‘peak’);
[upper_env_EMG2, ~] = envelope(rectified_EMG2, 80, ‘peak’);
% Convert and rescale the goniometer signal
rescaled_goniometer = (goniometerDatarfe – min(goniometerDatarfe)) * 120 /
(max(goniometerDatarfe) – min(goniometerDatarfe));
Get Biomedical Engineering assignment help in the UK from Ph.D. experts. Are you interested? Reach out to us at onlineassignmentservices1@gmail.com.
Question 4
In providing Biomedical Engineering assignment help for this question, OAS experts have analyzed the exhaustion process with the help of exhaustion Trial data. Additionally, the medfreq function has also been used to find each signal’s median frequency.
% Define the starting points of the 10s periods
start_times = [20, 40, 60, 80, 100, 120, 140];
% Define the duration of the 10s period
duration = 10;
% Calculate the corresponding indices for each starting point
start_indices = start_times * sampling_freq + 1;
% Initialize a cell array to store the extracted signals
extracted_signals = cell(1, numel(start_times));
% Extract the signals for each starting point
for i = 1:numel(start_times)
start_index = start_indices(i);
end_index = start_index + duration * sampling_freq – 1;
Want to buy MTE-40031 assignment help from the best subject matter experts in the UK? You are at the right place! WhatsApp us at +447700174710 today!
Question 5
In order to explain and arrange the code, our experts have written it as a MATLAB script with comments. Additionally, figures have also been plotted using the proper axis, figure, and legend names to provide the best MSc Biomedical Engineering Assignment Help to our students in the UK.
Explanation of fatigue Process
%The decrease in median frequency over time can be used to explain the fatigue process in the muscle activity. Median frequency is a measure of the central frequency of a signal and is commonly used as an indicator of muscle fatigue. % During muscle fatigue, there are several physiological changes that occur, including a decrease in muscle fiber recruitment, reduced muscle force production, and changes in muscle fiber conduction velocity. These changes can affect the frequency content of the electromyographic (EMG) signal. % As the muscle fatigues, the lower frequency components of the EMG signal become more dominant, leading to a decrease in the median frequency. This shift towards lower frequencies is associated with the recruitment of slower motor units and the activation of a larger number of muscle fibers to compensate for the fatigue-induced decline in force production.
Are you looking for the Best biomedical engineering assignment help in England? Call us at +61 871501720.

